Understanding Cosine Distance: A Detailed Guide

When we measure the similarity between two objects, we often consider their physical distance. However, in mathematics, computer science, and machine learning, there is a different approach to measuring similarity, and one of the most popular methods is cosine distance. This technique allows us to analyze how similar two items are, especially when represented in a high-dimensional space, such as text or images.

This article will explore cosine distance, why it’s essential, and how it’s used across various industries. By the end, you’ll understand the topic and how it fits into data analysis and machine learning.

What is Cosine Distance?

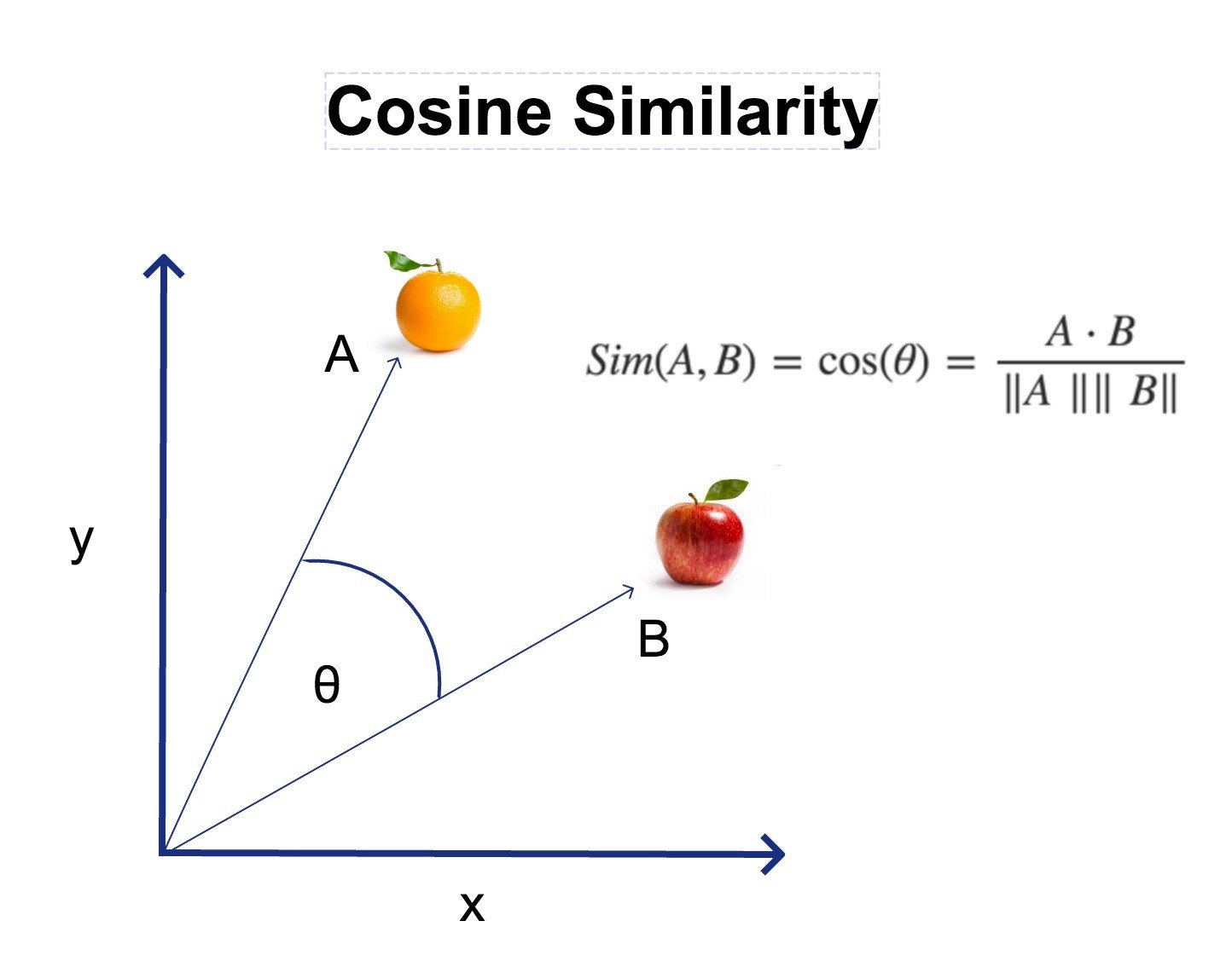
Cosine distance measures the angle between two vectors in a multidimensional space. Unlike Euclidean distance, which looks at the physical distance between points, cosine distance focuses on the direction of the vectors. In simpler terms, it evaluates how two items point in the same or opposite direction, regardless of size.

The formula for cosine distance is derived from the cosine similarity formula, where the similarity between two vectors is the cosine of the angle between them. Cosine distance is simply the inverse of cosine similarity and is often used to understand the degree of dissimilarity between two objects.

• Cosine similarity ranges from -1 to 1, with 1 indicating identical vectors, 0 meaning orthogonal (completely different), and -1 showing opposed.
• Cosine distance, on the other hand, is often defined as 1−cosine similarity1 – \text{cosine similarity}1−cosine similarity, transforming the range to [0, 2], where 0 means they are exactly similar, and 2 indicates complete dissimilarity.

Why Is Cosine Distance Important?

Cosine distance is widely used, particularly in text analysis, image recognition, and machine learning, because it is not affected by the magnitude of the vectors. In other words, even if two vectors are of different lengths, cosine distance still provides a clear view of their orientation and similarity. This makes it perfect for comparing data where size or scale should not be a factor, such as document similarity or user behavior in large datasets.

The Mathematics Behind Cosine Distance

To calculate cosine distance, we start by computing the dot product of two vectors, which gives a scalar value. Then, we divide that by the product of the vectors’ magnitudes (or lengths).

The formula is as follows:

Cosine Similarity=A⋅B∣∣A∣∣⋅∣∣B∣∣\text{Cosine Similarity} = \frac{A \cdot B}{||A|| \cdot ||B||}Cosine Similarity=∣∣A∣∣⋅∣∣B∣∣A⋅B​

Where:

• ABA \cdot BA⋅B is the dot product of the vectors A and B.
• ∣∣A∣∣||A||∣∣A∣∣ and ∣∣B∣∣||B||∣∣B∣∣ are the magnitudes of vectors A and B, respectively

To convert cosine similarity to cosine distance, the formula is:

Cosine Distance=1−Cosine Similarity\text{Cosine Distance} = 1 – \text{Cosine Similarity}Cosine Distance=1−Cosine Similarity

Example of Cosine Distance Calculation

Imagine you have two vectors: A = (1, 2, 3) and B = (4, 5, 6). The first step is to calculate their dot product, which is:

A⋅B=(1×4)+(2×5)+(3×6)=4+10+18=32A \cdot B = (1 \times 4) + (2 \times 5) + (3 \times 6) = 4 + 10 + 18 = 32A⋅B=(1×4)+(2×5)+(3×6)=4+10+18=32

Next, calculate the magnitude of each vector:

∣∣A∣∣=12+22+32=1+4+9=14||A|| = \sqrt{1^2 + 2^2 + 3^2} = \sqrt{1 + 4 + 9} = \sqrt{14}∣∣A∣∣=12+22+32​=1+4+9​=14​ ∣∣B∣∣=42+52+62=16+25+36=77||B|| = \sqrt{4^2 + 5^2 + 6^2} = \sqrt{16 + 25 + 36} = \sqrt{77}∣∣B∣∣=42+52+62​=16+25+36​=77​

Finally, plug these values into the cosine similarity formula:

Cosine Similarity=3214×77≈0.9746\text{Cosine Similarity} = \frac{32}{\sqrt{14} \times \sqrt{77}} \approx 0.9746Cosine Similarity=14​×77​32​≈0.9746

To find cosine distance:

Cosine Distance=1−0.9746=0.0254\text{Cosine Distance} = 1 – 0.9746 = 0.0254Cosine Distance=1−0.9746=0.0254

This result shows that the two vectors are similar, with a small cosine distance of 0.0254.

Applications of Cosine Distance

1. Text Mining and Natural Language Processing

In text analysis, cosine distance is widely used to compare the similarity of documents. For instance, when comparing two documents, the words in the documents are often represented as high-dimensional vectors and cosine distance is used to find how similar these two documents are in content.

• Document Classification: Cosine distance helps classify documents by determining how closely related a document is to a particular category based on the similarity of its text content.
• Plagiarism Detection: By comparing the cosine distance between different text samples, it is possible to detect plagiarism or duplicated content.

1. Machine Learning and Data Clustering

In machine learning, cosine distance is frequently used in clustering algorithms, such as K-means, to group similar items together. Using cosine distance, we can ensure that items with similar features are grouped regardless of size. This is particularly useful in high-dimensional datasets like user behavior data or image recognition.

1. Recommendation Systems

Cosine distance also plays a crucial role in recommendation systems, where it helps determine the similarity between users or products. For example:

• User-User Similarity: In a movie recommendation system, cosine distance might be used to compare the viewing preferences of two users, suggesting movies that similar users enjoyed.
• Product-Product Similarity: Retailers might use cosine distance to identify products often bought together, making recommendations to shoppers.

Advantages of Cosine Distance

• Scale Independence: Since cosine distance only considers the orientation of the vectors, it is unaffected by the scale or magnitude of the data. This is especially useful in text analysis, where documents can vary significantly in length.
• Simplicity: The mathematics behind cosine distance is straightforward, making it easy to implement in various applications.
• Versatility: From text mining to recommendation systems, cosine distance is highly versatile and widely applicable in many fields.

Limitations of Cosine Distance

Despite its advantages, cosine distance does have some limitations:

• Sparse Data: In some cases, data can be sparse (i.e., many zeros), affecting the accuracy of cosine distance. For example, when comparing two documents, the cosine distance might not accurately reflect their similarity if one document contains many unique words.
• Not a True Metric: Since cosine distance is based on angles rather than physical distance, it does not satisfy all the properties of a true metric, such as the triangle inequality.

Table: Comparison Between Cosine Distance and Other Similarity Measures

MeasureTypeRangeBest for

Cosine Distance Directional Similarity [0, 2] Text analysis, user behavior

Euclidean Distance Physical Distance [0, ∞] Geometric data

Jaccard Similarity Set-based Similarity [0, 1] Sets and binary data

Manhattan Distance Path-based Distance [0, ∞] Grid-like data (e.g., maps)

How Cosine Distance is Used in Everyday Technology

Many popular technologies we interact with daily use cosine distance behind the scenes. Here are a few examples:

• Search Engines: When you search for something on Google, the search engine uses algorithms that rely on cosine distance to find the most relevant pages based on the content of your query.
• Social Media: Platforms like Facebook and Instagram use cosine distance in their recommendation algorithms to suggest friends or content based on your interactions.
• Music Streaming Services: Spotify and other music platforms use cosine distance to recommend songs that match your taste, comparing your listening history with other users.

Cosine Distance in Future Applications

As technology evolves, cosine distance will expand into new areas, such as artificial intelligence (AI), deep learning, and personalized medicine. Here are a few future possibilities:

• AI-Powered Personal Assistants: Cosine distance could enhance personal assistants like Siri or Alexa, allowing them to provide even more accurate suggestions based on user behavior.
• Healthcare: In personalized medicine, cosine distance can help compare patient data to recommend the most effective treatments based on similar cases.
• Smart Homes: With the rise of smart homes, cosine distance could be used to optimize device interactions, making homes more efficient and personalized to their occupants.

Conclusion

Cosine distance is a powerful and versatile tool in many fields, from natural language processing to recommendation systems. Its ability to measure similarity without being influenced by the size of the data makes it invaluable in high-dimensional spaces. Whether comparing documents, clustering data, or making product recommendations, cosine distance has proven to be a reliable and effective method for measuring similarity.

As technology advances, cosine distance will undoubtedly play an even more significant role in our everyday lives, powering everything from AI to personalized medicine. Understanding this concept broadens our knowledge of data analysis and opens the door to its potential applications.

With the constant development of machine learning and artificial intelligence, the importance of cosine distance will only continue to grow, making it an essential tool for the future.

You may also read

Happy Lamb Hot Pot